Introduction

Cancer is the quick development of unusual cells in the human body. Cancer-causing agents are the substances that cause cancer. A cancer-causing agent is a compound substance with specific molecules in tobacco smoke. It has the potential to spread to different pieces of the body. A portion of the side effects of this infection incorporate bumps, unusual dying, prolonger hacks, weight misfortune, and so on. Primary drivers for this malignant sickness are biting tobacco, stoutness, awful eating regimen, apathy, and more admission of liquor. This perilous sickness can be restored by a few medicines like a medical procedure, radiotherapy, chemotherapy, chemical treatment, designated treatment, and others. Anticancer medications are those that are utilized to fix the illness's supposed cancer, which incorporates alkylates and metabolites. The substance chart hypothesis is a discipline of numerical science that arrangements with substance charts that show substance framework. The synthetic diagram hypothesis offers to characterize topological indices on anticancer medications. In this work, a few medications are taken, and utilizing the degree-based estimations, not many topological indices are characterized on different anticancer medications to decide actual qualities what's more, compound responses related to them [1-3].

Doxorubicin (Dox) is an anthracycline antibiotic drug broadly utilized in the curing of tumorous cells. In any case, it is related to the event of unfavorable responses that restricts its clinical use. In this specific situation, the embodiment of Dox in micelles receptive to pH varieties has been demonstrated to be a system for the growth conveyance of the medication, with the possibility to increment restorative viability and lessen the harmful impacts. For the formal reason, the study is initiated for improvements in drug use for the treatment of cancer. Drugs' molecular structures can be used to evaluate their pharmacological potential. Numerous researchers have recently exploited topological indices or mathematical graphs to prepare synthetic compounds and to enhance the statistical properties of medications [4]. Important aspects of cheminformatics include quantitative structure-activity relationships (QSAR) and quantitative structure-property relationships (QSPR), a new science that has been developed with the aid of computer sciences, mathematics, and chemistry. These segments can further the study of the physicochemical properties of synthetic mixtures. A modeling technique called QSAR is used to identify the most effective and efficient networks and structures by analyzing the topology of networks and compound structures. QSPR is another modeling approach that uses a mathematical equation or expression to correlate network structural features. In addition, it offers a quantifiable link between network or chemical structural features. Because they are invariant, topological angles can be represented using graphs as numerical values. Chemical compounds are transformed into graphs in the chemical graph theory using atoms as the vertex and bonds as the edges [5]. To identify the physical characteristics of chemical compound structures, numerous topological indices have been devised.

The problem statement is first introduced in this work with anti-cancer medicinal Structures. These chemical structures are solved by topological invariants like KBSO indices introduced by Gutman in 2021 [6], QCIs introduced in 2022 by V.R. Kulli [7], and Dharwad indices introduced by V.R. Kulli in 2021 [8]. Secondly, review the literature and background, thirdly discuss the section on research methods, the fourth portion on data analysis, and the last section on writing the findings and drawing a conclusion.

The study has modeling ramifications for the disciplines of chemistry and pharmacy the purpose of chemical structures, is to improve the effectiveness of medicine used against cancer patients. The study can learn more about algebraic structures and apply QCIs and KBSO topological invariants to theoretically forecast hidden characteristics of diverse anticancer chemical compounds employed to treat cancer patients. The chemical tests observed that there was a solid association between a molecular structure's topology and its physical characteristics, chemical properties, and organic elements, like boiling point, melting point, and poisonousness of medications [9].

Objectives

The study solves the topology of the chemical network structure mathematically by graph theory. Furthermore, it modeled the chemical structure with the help of deduced mathematical results. It also enhanced the existing chemical structure used for cancer medicine, reduced their irregularities, and found side effect-free, stable compounds, and efficient chemical structures in the context of anti-cancerous medicine.

Hypothesis

The chemical structure is solved by graph theory after converting it into graphical form, producing mathematical results for modeling anti-cancerous chemical structures.

Research contribution statement

This research aims to optimize existing chemical structures for anti-cancerous drugs by analyzing topological invariants and graphing chemical network structures. It will develop QSPR and QSAR models, discover the relationship between lower and upper bounds, and provide design guidelines for chemists.

Important issues

Due to the incremental and fast nature of cancerous cells, no adequate solution has been found till now. No existing or new efficient anti-cancerous drug or chemical structure has been discovered.

Literature review

Doxorubicin (Dox) is an anthracycline anti-toxin generally utilized in the therapy of cancer, notwithstanding, it is related to the event of unfriendly responses or bioactivities in the human body that restricts its clinical use. In this particular situation, the DOX embodiment in micelles open to pH assortments has exhibited to be a framework for the development movement of the medicine, with the likelihood to increment healing practicality and to diminish the destructive effects. The pH-fragile micelles had the choice to quell disease improvement basically when they appeared differently concerning the micelles of tricky and non-pH [10]. The investigation of self-get-together cycles in polymer arrangements is the premise of a cutting-edge methodology for focusing on frameworks for different substrates. Thus, the utilization of twofold polymer/surfactant frameworks makes it conceivable to grow the scope of polymers for making drug conveyance frameworks. This article portrays the cycles of development of crossover micelles in light of H20─[BH20-COOH] and surfactant Triton X-100 [11]. Improvement of a straightforward technique to upgrade focusing on and hostile to cancer impact of the chemotherapeutic specialists in vivo is a significant issue. The growth restraint pace of Dap- Dox micelles came to 96%. Dap-Dox micelles additionally really repressed the development of bacteria. Taken together, Dap-based drug conveyance frameworks are capable and viable in cancer treatment [12]. Skin cancer is a disturbing worry because of expanded radiation and synthetic openness. Dox is a drug recommended for different cancers by parenteral course. The created nanometric and symmetric transporters offered significant drug stacking, in addition offered a fleeting drug discharge for extended lengths [13]. The pH-subordinate drug discharge guaranteed the spatial conveyance at the objective site, without loss of drug in the fundamental dissemination. The cancer cell poisonousness concentrates alongside the in vivo enemy of growth concentrates on laying out the predominant viability of the created framework. The biochemical tests and blood profile investigations affirmed the well-being of the created nanocarriers. A lesser measure of the drug was accessible for the microsomal debasement, as surmised by the biodistribution studies. The discoveries give proof of idea to the more secure and compelling Dox conveyance utilizing basic excipients like phospholipids for the administration of skin cancer [14, 15]. Under acidic circumstances, the blended micelles expand and can deliver their payloads [16]. This particular cancer collection brings about a magnificent hindrance of in vivo growth development and a high pace of apoptosis in cancerous tissues, with low poisonousness. This profoundly steady, blended micellar framework with a pH-subordinate drug discharge, which empowers the exact conveyance of drugs to the growth sores, is practical to utilize clinically in cancer treatment. Gao et al developed several topological indices for the graphene and chemical amalgams used for the curing of tumors [17]. Kimrani reported topological indices for many antiviral drugs via M-polynomial and NM-polynomials and discovered the anti-cancer properties against cancerous cells [18]. Artificial intelligence has revolutionized the healthcare sector, enhancing diagnostics and clinical technologies. Today, e-healthcare is prevalent, allowing doctors to provide patients with personalized care, including the diagnosis of brain tumors [19]. Grade 1 and Grade 2 brain tumors can be cured after treatment, while Grade 3 or 4 tumors have high growth and spread. The goal is to accurately detect brain tumors at these stages using MRI images, as 90% of patients die when detected at stage 3 or 4 [20]. The study focuses on distinguishing cancerous cells in the human psyche from MRI images, using a planned U-Net (LU-Net) for recognition, arranging cerebrum MRIs into classes, and preparing deep neural models quickly [21, 22]. Drug repositioning has expanded considerably since the previous ten years as a few blockbuster drugs have emerged from repositioning. Computational methodologies are essentially adding to these endeavors, of which, network-based techniques assume a key part [23]. Phenotypic (non-hereditary) heterogeneity has huge ramifications for the turn of events and development of organs, creatures, and populations. Late perceptions in numerous cancers play an unwound part in phenotypic heterogeneity in driving metastasis and treatment unmanageability. In any case, the beginnings of such phenotypic heterogeneity are inadequately grasped in many cancers. Here, we research an administrative organization's basic phenotypic heterogeneity in little cell cellular breakdown in the lungs, a staggering sickness with no molecular designated treatment. Discrete and persistent dynamical recreations of this organization uncover a metastable way of behaving that can make sense of the concurrence of four tentatively noticed aggregates. Examination of the organization's geography uncovers that metastability rises out of two groups of players that commonly repress one another, yet individuals from a group enact each other, shaping a 'flip switch' between the two groups. Translating these topological marks in cancer-related administrative organizations can unwind their ''dormant'' plan standards and deal with an objective way to describe phenotypic heterogeneity in growth [24]. As the market for the customized cellular breakdown in lung medication extends, the interest in molecular demonstrative devices by and large, and strategies for distinguishing various qualities with subjective, quantitative, and high explicitness specifically, have developed. Here, we propose a framework for the successful identification of cellular breakdown in the lung's explicit, long-length epidermal development factor receptor (EGFR) quality changes by utilizing a topological change nano-barcoding procedure TNT. In a previous TNT review, EGFR was effectively distinguished in cell conditions and at test stages within the sight of reference quality. Nonetheless, because normal EGFR target focuses are fundamentally lower at the clinical stage and the test-restricting capacity of long-length targets is brought down that of short focuses, our framework utilizes polymerase chain response (PCR) enhancement, limitation, and sifting PRF for EGFR discontinuity to expand execution. In a PRF framework, the objective is enhanced by PCR, sliced to a reasonable size by a limited chemical, and separated by an attractive globule. With recognition cutoff points of 0.3555 % and 1.500 % for EGFR Del 19 and L858R transformations, separately, the proposed TNT with PRF can recognize freak cell lines and proficiently distinguish different lengths of hereditary varieties in clinical preliminaries [25].

Gathering proof demonstrates provincial primary changes in the white matter (WM) of cerebrums in patients with Blepharospasm (BSP); be that as it may, whether huge scope WM underlying organizations go through far-reaching rearrangement in these patients stays muddled. The review explored geography changes and worldwide and neighborhood highlights of enormous scope WM primary organizations in BSP patients contrasted and hemifacial fit (HFS) patients or sound controls (HCs) [26]. Topological techniques have as of late arisen as a solid and interpretable structure for extricating data from high-layered information, prompting the production of a part of applied math called Topological Data Analysis (TDA). From that point forward, TDA has been continuously embraced in biomedical exploration. Natural information assortment can result in colossal datasets, containing huge numbers of highlights and crossing different datatypes. The hindrance to beginning information examination as the central structure of the dataset becomes covered up, discouraging the revelation of significant highlights and examples. TDA answers get the fundamental state of datasets over consistent goals, relating to key topological elements free of commotion. TDA can uphold future improvements in medical services and utilize them to uncover stowed-away subgroups of cancer patients, develop authoritative guides of mind action, and order strange examples in clinical pictures [27]. The use of TDA is expansive and to comprehend where current accomplishments lie, the study assessed the current situation with TDA in cancer information examination [28].

Network medication gives network hypothetical devices, techniques, and properties to concentrate on basic regulations overseeing human interactome to distinguish sickness states and infection intricacy prompting drug disclosure. Inside this system. The OCN built from the tentatively confirmed qualities displays a fractal nature in the topological properties with well-established utilitarian networks demonstrating a self-putting-together way of behaving. The organization properties at all degrees of association submit to one boundary scaling regulation which needs a centrality lethality rule. We showed that ⟨k⟩ can be taken as a scaling boundary, where the power regulation example can be assessed from the proportion of organization widths.

In OCN, commonplace and connector center points, which incorporate recognized key controllers, assume significant liability to keep the OCN respectability and association. Furthermore, the vast majority of the key controllers are viewed as over-communicated and emphatically corresponded with resistant penetrates. At long last, not many potential drugs are distinguished and connected with the key controllers [29].

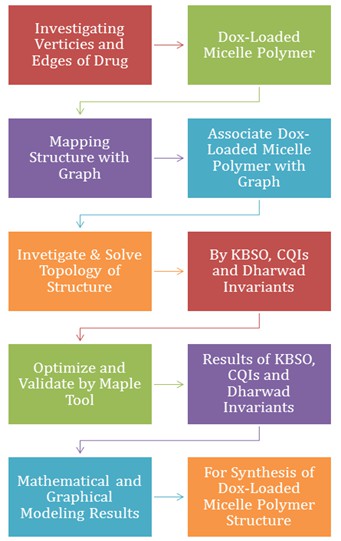
Figure 1: Research method

Materials and Method

With the aid of KBSO indices, QCIs, Dharwad indexes, and their reduced variants, this methodical study will take an existing anti-cancer medicinal structure, relate it to a graph, and resolve the graph's topology. Formula-based outcomes that are optimized will be compared to earlier findings. These inferred conclusions will be applied to modeling and improving the efficacy of medicinal structures used for cancer treatment. This model is quite effective because it accurately predicts results while solving the topology of a cancer drug in numerical and graphical form. After analysis, data are verified and validated using the simulation tool Maple [30-35].

Experimental results

Anticancer medicine is associated with graphs and solved through the KBSO index, CQIs, Dharwad index, and their other forms.

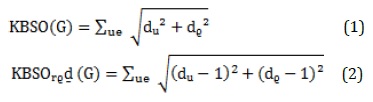
The KBSO index and its simplified form, which will be utilized to solve the cancer problem, are shown in Equations (1) and (2) [36-38].

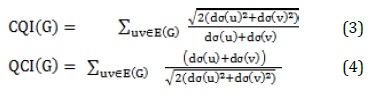
The CQI and QCI that will be employed for the solution of anti-cancer pharmaceutical structures are shown in Equations (3) and (4).

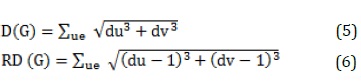
The shortened form of the Dharwad index with its original one which will be employed for the solution of anti-cancer pharmaceutical compounds is shown in Equations (5) and (6) [39, 40].

Table 1: Edge partition of the graph of the Dox-loaded micelle polymer as an anti-cancer medicine

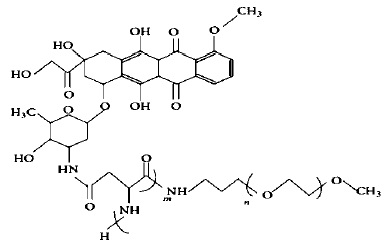
Figure 2: Molecular structure of anti-cancer medicine (Dox-loaded micelle polymer)

Table 1 indicates the graph's edge partitions of the anticancer medicine Dox-loaded micelle polymer given in Figure 2. There are eight distinct types of edges present in different vertices. On the other hand, frequencies of these concerning edges are presented in Table 1.

Main results of anti-cancer medicinal network

Figure 2 demonstrates the anticancer medicinal structure with bonds as edges and atoms as vertices. The molecular structure has an ‘n’ number of molecules in it. This molecular structure is used to solve Using topological invariants for the improvement of anti-cancer medicine. The hexagonal blocks show a benzenic ring, OH is the hydroxyl group, CH₃ is the methyl group, NH is the amine group, the double bond is the ketonic group, and Oxygen between two bonds is the esters group [41-45]. Based on the above figure, vertices show carbon atoms and lines or edges reveal bonds between atoms.

Figure 3 illustrated the anticancer medicinal structure with atoms as vertices and bonds as edges. The molecular structure has n=1 number of molecules means one molecule only. This molecular structure is a unit of anti-cancer medicine. The hexagonal blocks show a benzenic ring, OH is the hydroxyl group, CH₃ is the methyl group, NH and NH₂ are amine groups, oxygen double bond between two carbon atoms is the ketonic group and oxygen between two bonds is the esters group. From the above figure, vertices indicate carbon atoms and lines or edges show bonds between atoms.

Figure 4 depicts the anti-cancer medicinal structure with atoms as vertices and bonds as edges. The molecular structure has n=2 numbers of molecules meaning two molecules. This molecular structure is a part of anti-cancer medicine. The hexagon shows a benzenic ring, OH is the hydroxyl group, CH₃ is the methyl group, NH and NH₂ are amine groups, the oxygen double bond between two carbon atoms is the ketonic group and the oxygen between two bonds is the esters group. From the above figure, vertices show carbon atoms and lines or edges reveal bonds between atoms.

Figure 5 demonstrates the anti-cancer medicinal structure with atoms as vertices and bonds as edges. The molecular structure has n=3 numbers of molecules meaning three molecules. This molecular structure is a part of anti-cancer medicine which will be solved for the improvement of medicine. The vertices and edges are represented by carbon atoms and the bonds between them respectively. The NH/NH₂, CH₃, OH, and O are the following group's amines groups, methyl group, hydroxyl group, and oxygen respectively.

Dox-loaded micelle polymer graph        

Let G be the graph of Dox-loaded micelle polymer with edge partitions presented in Table 1.

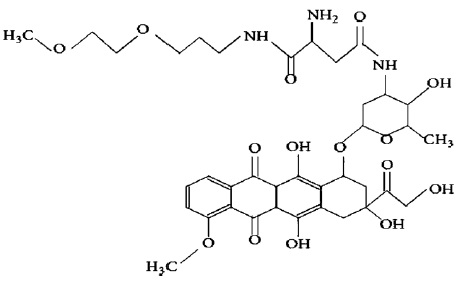
Figure 3: Molecular structure of anti-cancer medicine Dox-loaded micelle polymer with n=1

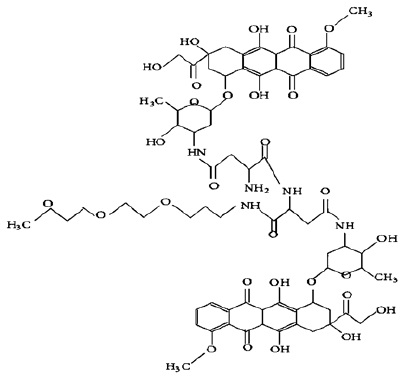
Figure 4: Molecular structure of anti-cancer medicine Dox-loaded micelle polymer with n=2

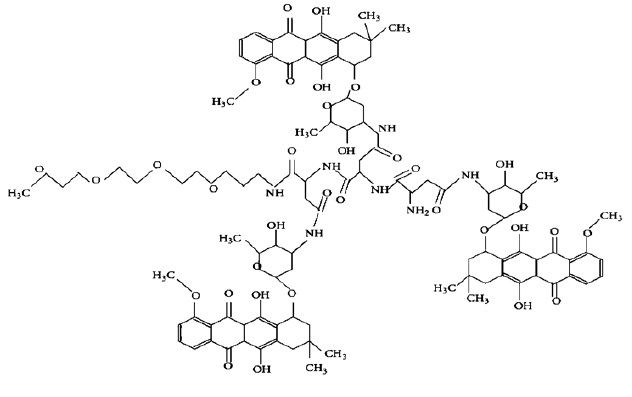
Figure 5: Molecular structure of anti-cancer medicine Dox-loaded micelle polymer with n=3

jTheorem 1

Let G = SP_n be a graph of Dox-loaded micelle polymer, then KBSO and KBSOred indices are described as follow:

KBSO(SP_n)=

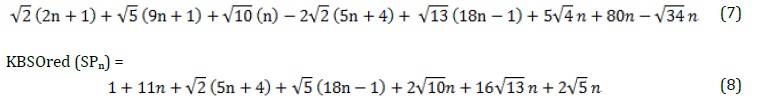
The graph's tested outcomes are represented by Equations (7) and (8) of the Dox-loaded Micelle Polymer mentioned in Figure 1.

Investigation of Dox-loaded micelle polymer graphs by KBSO indices

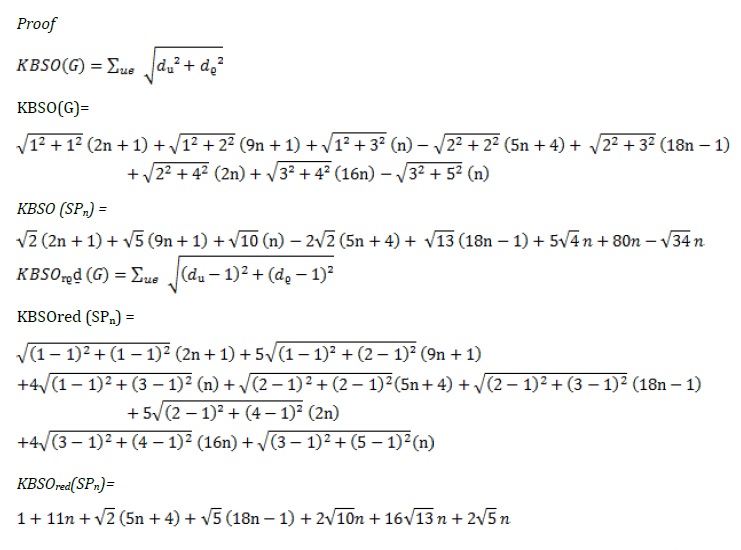
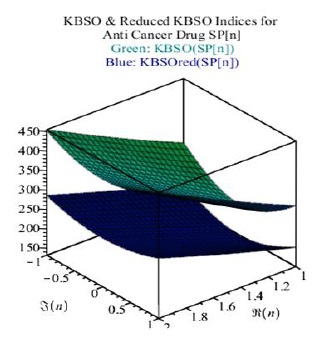
Figure 6: KBSO indices for Dox-loaded micelle polymer

Figure 6 shows the lower and upper bounds of the molecular graph after mapping through k-banhatti sombor invariants. These lower and upper bounds predict the reactivity, bond strength, melting, and boiling point in the human body.

Theorem 2

G will be a graph of Dox-loaded micelle polymer, then, CQI and QCI indices are as follow:

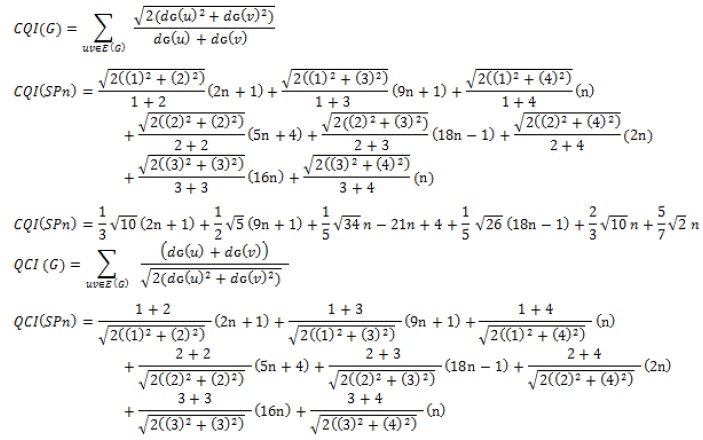
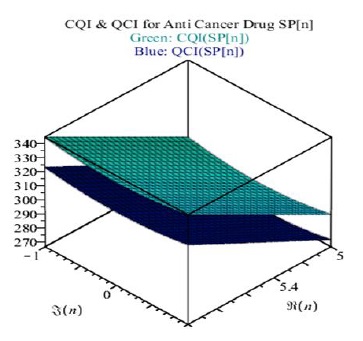
Figure 7: CQI and QCI for Dox-loaded micelle polymer

Figure 7 shows the lower and upper bounds of the molecular graph after mapping through Contraharmonic-quadratic invariants. These lower and upper bounds predict the reactivity, bond strength, melting, and boiling point in the human body.

Theorem 3<